Preliminaries

• Foreword
• Bit operations
  • Binary AND &
  • Binary OR |
  • Binary XOR ^
  • Invert ~
  • Not !
  • Shift <</>>
  • Exercises
    • Write a function that sets bits of source to value filtered by mask
    • Write a function that sets n-th bit of source to x
• Numeral systems
  • Decimal
  • Binary
  • Hexadecimal
• C knowledge
  • memcpy
• Electronics
  • Fundamentals
  • Basic safety
  • Signals and power rails
  • Signal and power rail naming
  • Common circuits

Foreword

This section contains a knowledge that we expect that you should already know. To ease the work in the course, we decided to give you materials even for this topics, as to give you a chance to catch up in case you missed something in your previous studies.

You can catch up to this during the semester, but if you are completely lost here, we cannot recommend the course for you.

Bit operations

Basic bit operations are necessary in low level C language when working on microcontrollers. They are used to mask values or set specific bits in values.

In this context, we refer to a mask as a value that tells use which bits are relevant. That is, mask has bit with value 0 if said bit is not relevant and bit with value of 1 if said bit is relevant. For example, if we want to work only with last 3 bits of one byte, the mask is 0000 0111

Binary AND &

Binary AND represents bitwise operation of anding individual bits.

Example: 1100
    &    1010
    =    1000

This operation is used to filter the required bits from a larger word. Lets say we need only first 4 bits from variable. Then we can use binary AND and a mask to do so.

Example: 1100 1101 0110 1001
    &    0000 0000 0000 1111
    =    0000 0000 0000 1001

C code example:

int i= 0b1100110101101001;
int mask = 0b0000000000001111;
i = i & mask; /* i value is now 0b1001 */

Binary OR |

Binary OR represents bitwise operation of oring individual bits.

Example: 1100
    |    1010
    =    1110

This operation is used to set the required bits from a larger word. Lets say we want to set the first 4 bits from a variable. Then we can use binary OR to do so.

Example: 1100 1101 0110 1001
    |    0000 0000 0000 1111
    =    1100 1101 0110 1111

C code example:

int i= 0b1100110101101001;
int mask = 0b0000000000001111;
i = i | mask; /* i value is now 0b1100110101101111 */

Binary XOR ^

Binary XOR represents bitwise operation of xoring individual bits.

Example: 1100
    ^    1010
    =    0110

This operation is used in cryptographical operations and checksum checking, or only subword bit inversion. Let’s say we need to invert only first 4 bits from a variable. Then we can use binary XOR to do so.

Example: 1100 1101 0110 1001
    ^    0000 0000 0000 1111
    =    1100 1101 0110 0110

C code example:

int i= 0b1100110101101001;
int mask = 0b0000000000001111;
i = i ^ mask; /* i value is now 0b1100110101100110 */

Invert ~

Invert represents operation of inverting individual bits.

Example: 1100
    ~    
    =    0011

This operation is used in word inversion, sometimes can be used combined with AND and OR to get Negated AND and OR. Lets say we need to invert variable. Then we can use invert to do so.

Example: 1100_1101_0110_1001
    ~    
    =    0011_0010_1001_0110

C code example:

int i= 0b1100110101101001;
i = ~i; /* i value is now 0011_0010_1001_0110 */

Not !

Not represents operation of value inversion. A non-zero variable is inverted into zero, and zero value is inverted into non-zero (e.g one).

Example: 1100
    !    
    =       0

            0
    !    
    =       1

Warning: do not mistake with invert, can you see the difference?

Shift <</>>

Binary shift is used to shift bits of the value either to the left or right.

Example: 1100_1101_0110_1001
    >>      5
    =    0000_0110_0110_1011

This in used when either reading value bit by bit or can be used to set n-th bit, where n is a variable.

C code example:

int i= 0b1100110101101001;
int offset = 5;
i = i >> offset; /* i value is now 0b0000011001101011 */

Exercises

Here are few simple exercises to practice bit operations. Implement them only with the help of &,|,^,~,!,<<, or >>, avoid any cycles.

Write a function that sets bits of source to value filtered by mask

uint32_t set(uint32_t source,
             uint32_t value,
             uint32_t mask)
{
    // return source such that: 
    // forall i: if mask[i]: source[i] = value[i]
}

Write a function that sets n-th bit of source to x

uint32_t set_bit(uint32_t source, uint8_t n, uint8_t x)
{
    // set `n-th` bit of `source` to `x`
}

Numeral systems

Number is a value that is represented in binary format in the device and in multiple other forms in the source code. Keep in mind that the representation such as 42 in int i = 42 is not a number, that is just a representation of the number.

Most relevant ways of preresentation are: decimal, hexadecimal, and binary.

In the embedded world, we want to focus on hexadecimal system rather than decimal. That is partially done out of habit and partially because we are more interested in the binary representation of number and it is easier to translate hexadecimal numbers into their binary representation.

Decimal

Decimal numbers are the numbers we all learn in chool and commonly use. One of the reasons we use the decimal system is the fact that we have 10 fingers. When we write number in C we are most commonly using the decimal numbering system as it is the default.

Radix of decimal numbers is 10

Binary

Binary numbers are the representation used by our microcontrollers. The reason for that is that our modern computers are good at processing simple on/off states which lead to building a binary system of operations.

Radix of binary numbers is 2

Use: binary numbers are rarely used in programming because it is difficult for humans to read such numbers. If they are used, in C language the number must be prefixed with 0b to tell that the number is binary.

Conversion: Conversion from decimal number to binary number is pretty common, but lets refresh the process:

    dec -> bin : 
    1234 / 2 = 617 ; 0 
     617 / 2 = 308 ; 1 
     308 / 2 = 154 ; 0 
     154 / 2 = 77  ; 0 
     77  / 2 = 38  ; 1 
     38  / 2 = 19  ; 0 
     19  / 2 = 9   ; 1 
      9  / 2 = 4   ; 1 
      4  / 2 = 2   ; 0 
      2  / 2 = 1   ; 0 
      1  / 2 = 0   ; 1 
                    1234 -> 100 1101 0010

We assume that you know how this process works, if not, please do refresh your memory. The same can be done in other direction, just use multiply instead.

Hexadecimal

Hexadecimal numbers are the most favored in embedded, the reason as stated above is that it is easier to translate a number into binary form. For that, you just have to realize that each hexadecimal digit represents 4 bits in binary. That is, we just make a simple table that tells us 4 bits of any hexadecimal digit.

Hexadecimal numbers have radix of 16.

As our numbering system has only 10 digit symbols, we use characters A-10 B-11 C-12 D-13 E-14 F-15 for the remaining digits.

Conversion:

    dec -> hex
    1234 / 16 = 77 ; 2 
      77 / 16 =  4 ; D 
       4 / 16 =  0 ; 4 
    1234 -> 4D2

    bin -> hex
    0100 1101 0010
     4    D    2 

You can see how the bin -> hex conversion is much simpler

When we want to write hex number in C language it must be appended 0x to the front of the number - 0x4D2

C knowledge

We assume that you had a course with introduction into low level programming and that you experienced development in C in your life. The course focuses on basic usage of C, and we avoid going into a depth of the more advanced topics.

Out of that, there are some key points that we want to note, out of our experience of what students commonly missed.

memcpy

void* memcpy(void* dest, void* src, size_t count); is a function provided by standard library (in file string.h, which is not intuitive). The function copies count bytes from dest into src.

That is, instead of writing:

uint16_t input_buffer[64];
uint16_t output_buffer[64];

for(uint32_t i = 0; i < 64; i++){
    output_buffer[i] = input_buffer[i];
}

we can simplify the code a bit:

memcpy(&output_buffer, 
       &input_buffer, 
       64 * sizeof(uint16_t));

In embedded, copying of buffers is frequent operation, as we tend to use one buffer for storing input data and different buffer for processing of data from previous frame.

Electronics

As this course works with microprocessors on a quite low level, we will directly interact with the electronics on the board or even connect modules with wires. This requires atleast a very basic knowledge (high school level) of electronics. We will work exclusively with DC (Direct current) signals and power, so we are not going to go into detail on AC (Alternating current). Let’s go through the fundamentals, some basic safety and principles of how signals work.

Fundamentals

We will first define a charge, which is some energy stored at some point (it is carried by electrons, which carry elementary charge). It’s base unit is Couloumb.

Let’s base all our knowledge on the Ohm’s law U = I * R, where:

• U is voltage (base unit Volts). Voltage is the potential of a charge at any given point. Take note that voltage is always a relative measurement and it can be negative! We need to select some potential as 0V, usually called a ground. We then measure against this potential.
• I is current (base unit Amperes). This is the amount of charge per second which flows from one point to other.
• R is resistance (base unit Ohms). It is the “force” that limits the amount of current between two potentials.

We can deduce some basic principles of how electricity acts from this:

• Charge flows from high potential to low potential. For example, from 3.3V source to ground through some light emitting diode. This is not directly from Ohm’s law, but makes sense, as the system wants to stabilize (achieve equilibrium).
• This flowing charge is limited by the resistance between high and low potential.
• The charge will always prefer the path of lower resistance.
• Higher resistance in the path leads to either lower current (if we have fixed voltage), or we have to increase the voltage to keep the current.
• We can always calculate the third variable if we know the other two (extremely basic math!).
• In reality, the actual physical charge (electrons) go from low voltage to high voltage, as they carry negative charge. (Conventional vs actual flow of electricity).

Usually, in any circuit, we will have a fixed voltage as a main source (in our context, most often 3.3V or 5V) and changing resistance (most digital parts constantly change their innner resistance as they work). Thus the current will also change.

We can also calculate a current power usage if we know the source voltage and total current flowing: P = U * I, where P is power in Watts. In most digital circuits, all the power going into the device in converted to heat with 100% efficiency. Anything above 1 Watt will usually heat up quite a lot and can burn you!

All this holds only for DC (direct current) circuits! To understand AC, we would have to expend another few chapters here, and it is not necesarry for this course.

Basic safety

Electricity can easily kill you even with seemingly low numbers. Common safe voltage is anywhere from 0 to 60 volts (only applicable to direct current). A very low current going through your body (more specifically your heart) can kill you - few milliamperes is enough. Usually a fairly large voltage is required for this, usually above 60 volts.

Although the “safe” voltage is up to 60 volts, you still need to be cautious when working with low voltage levels. A 3.7V li-ion battery can store similar amount of an energy as a stick of dynamite, and can release it very quickly, even when it is a low voltage device. A typical welding machine can provide tens to hundrends of amps, but at low voltage. You always need to take into consideration the overall power capabilities of the system.

Let’s define some basic rules that you should follow when connecting anything together and working with low voltage devices we will use:

1. Always have properly grounded devices, for protection of yourself. Otherwise you risk that during a malfunction, your body will be the path of least resistance for the electricity. Most modern devices should be okay only with plugged in power, as they will ground themselves through the power cable.
2. Be cautious about static electricity that you might generate. The static charge can reach 100 thousands of volts (and yet wont kill you, as it is very quick current pulse when discharged). Some devices are very sensitive to high voltages, so if you are prone to charging up, you should touch some grounded part to discharge yourself before touching the electronics. Touching a metal leg of a table or the case of a desktop computer is usually enough.
3. When connecting power with wires (not using a connector like USB or such), double or even triple check that you are not reversing the polarity - switching ground and a voltage source when connecting a device to a power supply. Ie, connecting power supply ground to device power and power supply voltage to device ground. Reverse polarity can at worst completely destroy both the device and the power supply.
4. When powering anything that can consume more than a watt of power, be careful about the heat that might get produced so that you don’t burn yourself. A small chip using 2.5 Watts can heat up to about 80-90 degrees Celsius very easily.
5. In general, be cautious when touching powered electronics, so that you don’t accidently short something or get shocked.
6. When using a lab power supply (one that has customizable voltage and current limit), don’t turn on the power output with the settings on the max value. First set them to correct values and setup the current such that it’s just what the device requires, then turn the power output on. This way you prevent possible damage to a device.
7. This course is no means a tutorial or a substitute for any actual electronics course. You might try some DIY projects with Arduino at such, but you most definitely lack any knowledge to work with high voltage/power, most importantly mains power (230 V AC). Any mistake in a 3.3V design will probably result in just some smoke, a mistake with a 230V power supply will easily result in a fire, damage, substantial injuries or death.
8. When you are not sure on how to connect something together, rather than trying various combinations until it works, either consult documentation or someone who has the knowledge. Hardware has no undo!

Signals and power rails

When connecting devices together, we usually talk about electrical connections as signals and power rails. The difference between these is quite simple: a signal is for data (or/and signaling events), power rails are for power connections (the naming comes from the time when power rail was quite liteally a rail of metal).

When talking about power rails, we usually care about 2 main parameters:

• the voltage - in our course we will almost exclusively work with 3.3V, sometimes 5V power rails. For reference, USB provides 5V.
• the maximum current it can provide - given in amperes. For reference, USB, by default, can supply 500mA. We will only work with Constant Voltage power rails, which keep their voltage at the same level, and provide as much current as given by the load’s (connected device) resistance. Some power supplies will shutdown when you request more current than needed, other will get damaged.

When connecting power rails, you should always take care to match up the voltage - when device requires 3.3V, you should not use anything above 3.3V, as that might damage it. Supplying lower voltage than required might or might not work, depending on device’s operating range. Most modern devices have operating range with some tolerance (for example from 1.8V to 3.6V), but nowadays industry “standardized” on few common low voltage power rails: 1.8V, 3.3V and 5V.

We usually take ground as another power rail which supplies 0V and can sink (absorb) infinite current (this is a big simplification, but enough for our course).

Most modern devices requires constant voltage source and have their power consumption listed (either in watts or amperes). When picking a power source for a device, we need to provide a power rail which has the desired voltage, and current/power rating equal a higher.

For signals, we care about more parameters:

• signal type - digital, analog or any other (described later)
• voltage levels - what are the typical voltage levels (ie what is logical 0, logical 1), if the signal is differential, etc.
• protocol used (if any)
• frequency of the signal - the speed at which the voltage levels change, usually in Hertz For signals, we mostly just use the voltage on the wire/cable as the main information. Thus we don’t care about the current rating, as only minimal current will flow. Although there are exceptions to this. We mostly care about matching up the voltage levels, as a mismatch can damage either end of the connection. Most microcontrollers and sensors do not have any internal protection on their signal connections that would protect against an higher than usual voltage. We also obviously have to match up the protocol and signal type. If you connect two different protocols or signal types which operate with same voltage levels, you will most likely just either get garbage input/output or it just won’t work at all.

Digital vs Analog signals There are two main types of signals we will encounter.

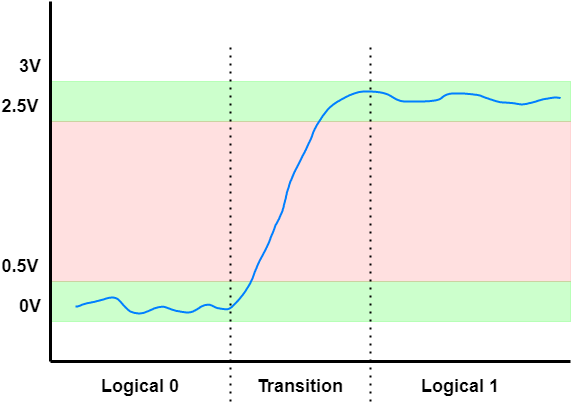
Digital signals are signals that have two distinct voltage levels defined, representing zero and one. We also usually define some range in middle that is not a defined and should only be used for transition of levels. Example: Let’s define a 3V digital signal such that anything above 2.5V is logical one, anything below 0.5V is logical zero. Then our undefined region is 0.5V - 2.5V.

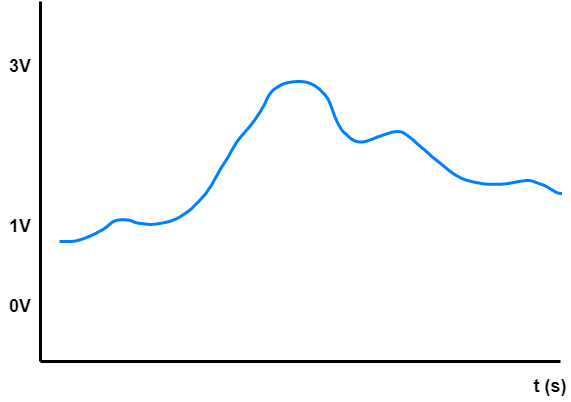
Analog signals are signals that are continuous in some defined range. They do not have distinct defined levels,but have infinite possible levels. Example: Let’s say we have a temperature sensor that outputs voltage in range 1V to 3V, where 1V is 10 degrees celsius and 3V is 30 degrees celsius. We then have infinite precision between these two maximums.

Nowadays, digital signals are used more often, as having only two valid levels is simple to design electronics with. They are less susceptible to interference and can usually achieve higher speeds than analog signals. Analog signals are more susceptible to interference, noise and the infinite precision is only a theoretical property that does not hold in real world. (From pure electronics and practical viewpoint, digital signals are still analog. When working with highspeed signals, everything is looked at as analog signal.)

Signal and power rail naming

You will meet some more-or-less standard names for some power rails and signals. This is not a big overview, mostly just of the names that you might come upon in this course.

Signals:

These are mostly dependent on the protocols used, so you will find these in the respective chapter for a protocol. There are some common acronyms used:

• CLK, CL will often refer to a clock signal, used for synchronization.
• DI, DO for data in and data out

Power rails:

GND for ground. You can also encounter VSS as ground in older or analog designs. You can also find GNDA, GNDB, GNDC as various separate grounds.

3V3, 1V8, 5V0 for defined voltage power rails. The V is used as a demical point. This comes from the fact that a small dot was hard to print to be readable historically. We also often use similar shorthands for

VDD, VCC, VBUS, VDDA as named power rails. Usually you have find out which voltage these are depending on the component/device used. For us, VDD will be often 3.3V, VBUS is usually 5V from a USB.

Common circuits

We will often encounter identical patterns when looking at electronics schematics. Let’s look at the three most common ones that you will encounter in this course.

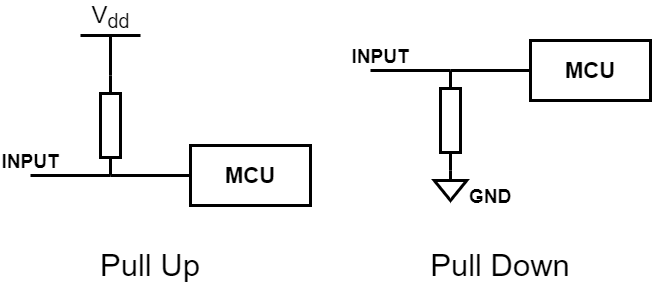
Pull-up, pull-down resistors

Pull up and down resistors are used to impose a default value on a signal line. In the following circuit, when INPUT is disconnected, there is no defined value on the line. Using a relatively high value resistor (1k ohms to 100 ohms) can be used to set a value on the line. Pull ups set logical one on the line, pull downs set logical zero. These resistors have low enough value that when the signal is connected, they will get “overrided” by the signal.

More circuits to be added soon.